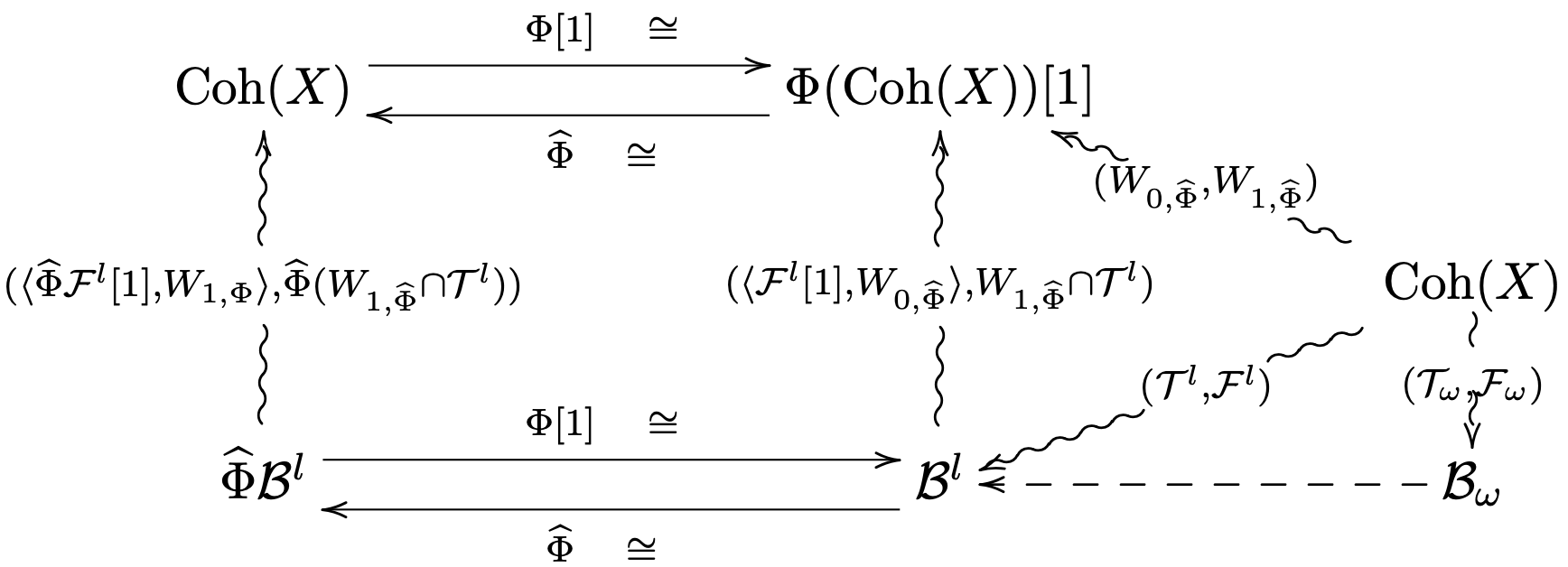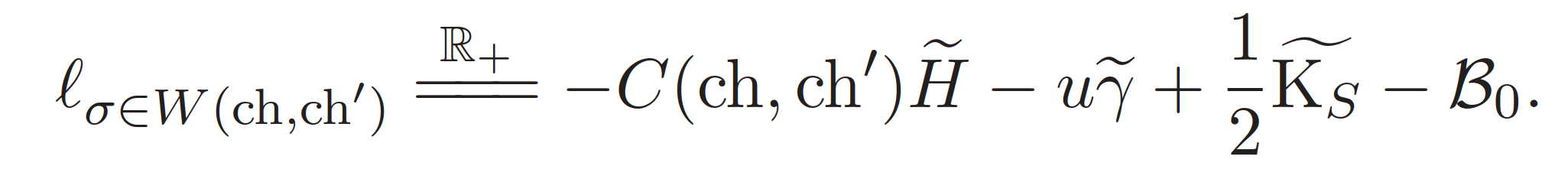Back to homepage.
Bridgeland stability condition – new aspects to symmetry and classification
The intertwinement of mathematics and physics is amazing. Many deep mathematical theories turn out to be foundations in physics such as Riemannian geometry to general relativity, while many beautiful ideas in physics turn out to be deep theories in mathematics such as string theory to modern algebraic geometry and symplectic geometry. The notion of Bridgeland stability condition, introduced by Bridgeland in 2002, is a perfect example.
What is a triangulated category?
Since the 1940s, mathematicians have upgraded the set theory to the category theory, where the former only concerns objects in it while the latter pays more attention to the relations among objects – mathematically called morphisms of objects. There is a good category, called abelian category, where we have the ability to say subobject and quotient object – actually morphisms with special types. Since the 1960s, a giant category has appeared – the triangulated category. We may imagine a triangulated category as a skyscraper with infinitely many floors – where such infinity are indexed by integers. So we could say -5th floor or 7th floor. We also assume all floors are the same so we can shift one floor to another. Moreover, the 0th floor is taken to be the abelian category. An object in a triangulated category becomes giant – it could have different components in different floors. To make an effort to say subobject and quotient object again, we need to put some triangle axioms into the giant category – this is the name of the triangulated category. There is still a notion of morphism – relations among objects. This way, the giant skyscraper - the triangulated category - has more objects and morphisms than its 0th floor alone - the abelian category. Such a mathematical notion turns out to be a precise playground for so-called D-brane in string theory, where objects in the triangulated category could be formally through as D-branes and morphisms could be thought of as open strings. All axioms in the triangulated category have physical meaning. In general, a t-structure on a triangulated category is a way to axiomatize the properties of abelian subcategories, and it is indexed by integers.
What is a Bridgeland stability condition?
A Bridgeland stability condition σ=(Z, P) on a triangulated category D consists of a central charge Z, which is a fancy way to measure different objects in D, and a slicing P, which is an real-number indexed refinement of t-structure on D. Moreover, the pair of data (Z, P) satisfies some axioms. Indeed, Z associates each object with a complex number, and we could use the phase of this complex number to compare objects in D. Putting all the complex numbers together, it forms a complex manifold – the Bridgeland stability manifold Stab(D).
Bridgeland stability condition brings new aspects to symmetry and classification.
Two central themes in mathematics are symmetry and classification. Bridgeland stability condition brings new aspects to both of them. On the one hand, the notion of Bridgeland stability condition updates our understanding about symmetry: it is a key notion for the understanding of Kontsevich’s Homological Mirror Symmetry, which is a deep categorical duality conjecture between algebraic geometry and symplectic geometry, and has been a major source of progress in mathematics. On the other hand, the notion of Bridgeland stability condition brings fresh ideas on the classification: many classification problems could be thought of as wall-crossing phenomena in different Bridgeland stability manifolds.
Bridgeland stability and derived category theory provide deep connections of different branches of mathematics. Some fundamental questions in algebraic geometry, which cannot be solved using the traditional method, have been solved by using Bridgeland stability condition.
The research on the notion of Bridgeland stability condition is very new and active and it attracts many talented young investigators. The purpose of my research is to create new understandings on the notion of Bridgeland stability condition, and find its new applications in Algebraic Geometry.
Reference
T. Bridgeland, Stability conditions on triangulated categories. Ann. of Math. (2) 166 (2007), no. 2, 317–345.
Last update on 04 March 2026.